Interleaving

The interleaving step in MixMatch is a little bit of a mystery. The paper doesn't go into detail about it at all, however, the TensorFlow implementation does use it.

This issue thread google-research/mixmatch/5 attempted to explain and justify the use of Interleave. However, it's unclear if it's a limitation of TensorFlow or a necessary step for good performance.

The Justification

Following the issue thread, Interleave creates a batch that is representative of the input data, as they "only update batch norm for the first batch, ..." Specifically, this batch should be of shape (B, C, H, W), where B is the batch size. This differs from the input of shape (B, K + 1, C, H, W), where K is the number of augmentations.

Interleave deterministically mixes the labelled and unlabelled data to create a new batch of shape (B, C, H, W).

Interleaving Process

This may sound a bit confusing, so let's review how we arrived at this step.

Recall that we only interleave the X Mix Up before prediction then reverse the interleaving after prediction.

Remember the shapes of the data.

Mix Up is just a proportional mix of the original data and a shuffled version of the data. Assuming a 32x32 RGB image, the shape of this X Mix:

It's confusing with words, so let's visualize what interleave does. Here, each cell is C x H x W with K = 2, B = 5

	B=0	B=1	B=3	B=4
K=0 Lab.	CxHxW	...
K=1 Unl. Aug 1	...			...
K=2 Unl. Aug 2			...	CxHxW

Given the constraint mentioned above, we can't use the first B x C x H x W for prediction, as B x K=0 x C x H x W would just yield the first K, which are all labelled data. This is not representative of X Mix.

Find all elements on the first augmentation

	Item 1	Item 2	Item 3	Item 4	Item 5
Lab.	O	O	O	O	O
Unl. Aug 1
Unl. Aug 2

Find all elements on the "diagonal", this is usually not a true diagonal as it's not perfectly square, we'll mark this as X.

	Item 1	Item 2	Item 3	Item 4	Item 5
Lab.	X	X
Unl. Aug 1			X	X
Unl. Aug 2					X

Swap these elements

	Item 1	Item 2	Item 3	Item 4	Item 5
Lab.	OX	OX	X	X	X
Unl. Aug 1			O	O
Unl. Aug 2					O

Notice that this interleaving process proportionally mixes the labelled and unlabelled data. This first row of shape (B, C, H, W) is then used to predict the labels of X Mix.

Reverse the interleaving process

	Item 1	Item 2	Item 3	Item 4	Item 5
Aug 1	OX	OX	O	O	O
Aug 2			X	X
Aug 3					X

This process is perfectly reversible.

Our Preliminary Results

We briefly tried this under 3 conditions:

With interleaving (the default implementation)
Without interleaving, across all augmentations
Batched across all augmentations

Our 2nd experiment is not subjected to the limitation mentioned above. We can just pass the splits into the model sequentially.

Our 3rd experiment concatenates the splits into a single batch (in our case we just didn't split it). This is the most representative of the data, as the model is trained on the entire batch. Due to our larger batch, we also multiplied the learning rate by (K + 1).

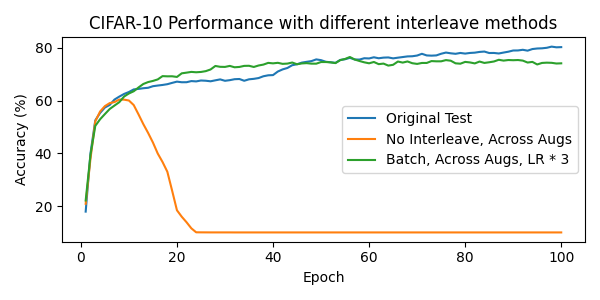
We can see that our 2nd experiment failed to converge, while our 1st and 3rd are comparable. We tease out possible issues in the next section.

BatchNorm is not order invariant

Let's dig a little deeper into BatchNorm, specifically, how the running mean and variance are calculated.

import torch
bn = torch.nn.BatchNorm1d(1, momentum=0.5)
bn(torch.ones(2, 1, 1))
print(bn.running_mean)  # 0.5
bn(torch.zeros(2, 1, 1))
print(bn.running_mean)  # 0.25

This outputs 0.5, 0.25 respectively, this is because

One can think of momentum as the weight of the new value, so a lower weight means a slower change in the running mean and variance. This algorithm only depends on the immediate previous value, this means that this can be a problem

import torch
bn = torch.nn.BatchNorm1d(1, momentum=0.5)
bn(torch.ones(2, 1, 1))
bn(torch.ones(2, 1, 1))
bn(torch.zeros(2, 1, 1))
print(bn.running_mean)  # 0.3750

bn = torch.nn.BatchNorm1d(1, momentum=0.5)
bn(torch.zeros(2, 1, 1))
bn(torch.ones(2, 1, 1))
bn(torch.ones(2, 1, 1))
print(bn.running_mean)  # 0.7500

Despite the same input, the running mean is different. This is reflective of our previous experiment, where we split the data into multiple batches to pass into the model sequentially, it's heavily biased against the first batch, which is our labelled data.

To fix this, instead of passing them in sequentially, we can pass them in a single batch. This is what we did in our 3rd experiment, and it has the same effect with the 1st experiment, where we interleaved the data.

To recap, these are how our 3 experiments passed the x_mix into the model.

import torch
bn = torch.nn.BatchNorm1d(...)

def interleave(x) -> torch.Tensor: ...

N_AUGS = 4
x_mix = torch.ones(2, N_AUGS, 1, 1)

# Experiment 1
x_mix = interleave(x_mix)
bn(x_mix[:, 0, ...])

# Experiment 2
for i in range(N_AUGS):
    bn(x_mix[:, i, ...])
    
# Experiment 3
bn(x_mix.reshape(-1, 1, 1))

Conclusion

It's inconclusive if interleaving is necessary, as passing the whole batch into the model has the same effect, and theoretically, more sound. However, it's clear that passing the data sequentially is not a good idea.

Last modified: 26 November 2023